|
Sections : International Standard Atmosphere (ISA) Variation due to Local Ground Conditions Variation of Density due to Humidity Variation of Density with Extremely High Altitude Tabulated Data : Table of Atmosphere Properties. Software : |
ISA VARIATION WITH ALTITUDEPressure, temperature, density, viscosity and speed of sound variation for the international standard atmosphere (ISA) can be calculated for a range of altitudes from sea level upward. This is done using an exact solution to the hydrostatic equation for a column of air. The air is assumed to be a perfect gas. In the lower region, the troposphere, the atmosphere has a lapse rate (L) of 6.5K/Km . At an altitude of 36089 ft the stratosphere starts and the temperature remains constant at 217K. The hydrostatic equation, perfect gas law and the lapse rate equations are, $${∂P}/{∂h} = - ρg\text" "P=ρRT\text" and "T=T_0-Lh$$ where the variables used are,
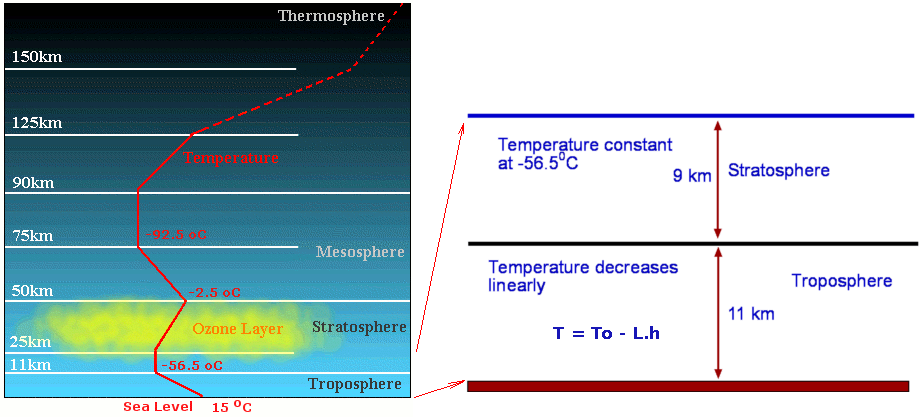 Atmospheric Layers and Temperature Variation with Altitude. Solving the hydrostatic equation with a constant lapse rate gives the resulting pressure variation in the troposphere. $$P/P_0=(T/T_0)^{g/{LR}}$$ where sea level pressure, $P_0$ , is set at the standard 101.3 kPa. Solving the hydrostatic equation with a constant temperature gives the resulting pressure variation in the stratosphere. $$P/P_s=e^{{g(h_s-h)}/{RT_s}}$$ where conditions with subscript ($s$) are values of altitude ($h_s$), pressure ($P_s$) or temperature ($T_s$) at the tropopause, the start of the stratosphere; the line dividing the two distinct atmospheric regions. Once pressure has been calculated at a particular altitude, density is then calculated using the perfect gas law. Viscosity and kinematic viscosity are found by applying the Sutherland law $$μ=0.1456×10^{-5}{√{T}}/{1+110/T}$$ And finally speed of sound is found based on the temperature, $$a=√{γRT}$$ where $γ$ is the ratio of specific heats for air (1.4)
|