Resources | Aerodynamics for Students

AIRCRAFT PERFORMANCE

Fixed Wing Aircraft

Properties of the Atmosphere

Aircraft Weight and Geometry

Airspeed Measurement

Lift and Lift Coefficient

Drag and Drag Coefficient

Engine Thrust and Power

Performance Envelopes

Weight and Balance Requirements

RANGE AND ENDURANCE

The range of the aircraft is a function of the rate at which fuel is being burnt, the duration of cruise, the flight speed and the aerodynamic performance during the flight. The mode of flight can also have a measurable effect on the distance traveled. Of major importance is the fact that the fuel used to supply the engines must be carried onboard the aircraft. This fuel weight must be supported by the aerodynamic lift along with the aircraft structural weight and the payload. While the structure and payload weights are fixed, the fuel weight changes significantly during the flight, leading to changing performance during long range cruise.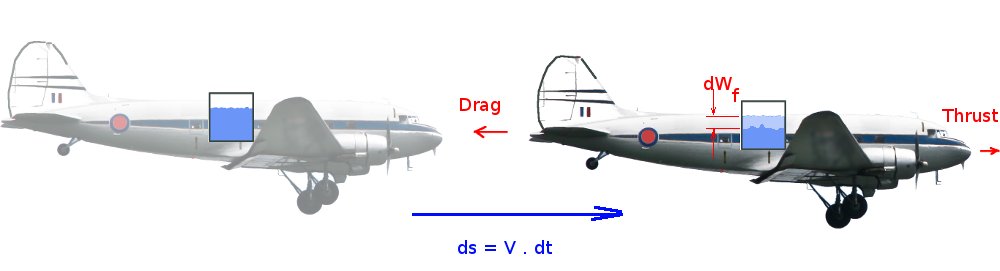

For cruise performance in level flight the excess power goes to zero. It is then a problem of analyzing the aircraft internal energy balance. The balance of energy being created by the combustion of fuel and the energy dissipated in overcoming the resistance to motion through the air.

For a short period of time, $dt$, while the aircraft moves a distance, $ds$, at a velocity $V$,

so that, $ds = V.dt$, if the energy is balanced then,

Energy(combustion of fuel) = Energy(dissipated by drag)

that is

Energy_in=Energy_out

Energy IN

$$ E_{in} = \text"Energy obtained from fuel combustion" = dW_b H_c η$$

where $dW_b$ is weight of fuel burnt during time $dt$, $H_c$ is energy content (calorific value) of fuel and $η$ is the overall efficiency of the propulsion system.

This is also equivalent to the Energy produced (Work Done) by the propulsion system over the time step

$$E_{in}=TV.dt$$

where $T$ is the thrust produced, $V$ is the flight velocity, hence $T.V$ is the supplied power over time $dt$.

Thus $ TV.dt = dW_b H_c η $

Rearranging this term into parameters that are readily able to be measured gives

$$H_cη=TV {dt}/{dW_b} = V/{{dW_b\/dt}/T}=V/{TSFC}$$

where, $TSFC$ is thrust specific fuel consumption, and is normally available from engine manufacturer tests.

Energy OUT

$$E_{out}=\text"Enery dissipated due to aircraft motion"=DV.dt$$

where $D$ is drag on the vehicle, $V$ is flight velocity, hence $D.V$ is required power to be overcome during time $dt$.

Energy Balance

This balance of energy components $E_{in}= E_{out}$ gives,

$$V/{TSFC}dW_b-DV.dt =0$$

If there is excess thrust over drag then an excess of energy will be availble to change the motion of the aircraft.

$$V/{TSFC}dW_b - DV.dt=ΔE$$

In terms of specific energy, $E\/W$, normally called energy height, $h_e$,

$${ΔE}/W=V/{TSFC}{dW_b}/W-D/WV.dt=Δh_e$$

Rearranging gives,

$$V/{TSFC}{dW_b}/W -D/W.ds - Δh_e=0$$

Based on the assumption of level flight, $L = W$, the assumption of roughly constant altitude and velocity cruise, $Δh_e ≈ 0$ . If the change in weight of the vehicle is directly related to the weight of fuel burnt, $dW_b = -dW$ , then

$$V/{TSFC}{-dW}/W - D/W.ds =0$$

$$ds={-V}/{TSFC}W/D{dW}/W = {-V/{TSFC}L/D{dW}/W$$

Assuming approximate steady conditions where velocity and propulsion performance is kept constant and that the aerodynamic parameter $L\/D$ is maintained at a constant value then integration of this equation from initial weight ($W_i$} to final weight ($W_f$) gives a prediction of range,

$$R = ∫.ds = ∫_{W_i}^{W_f} {-V}/{TSFC}L/D {dW}/W$$

$$R = {-V}/{TSFC}L/D ∫_{W_i}^{W_f} 1/W .dW$$

$$R=V/{TSFC}L/D ln(W_i/W_f)$$

This is the classic Breuget Range equation. It can be used to give reasonable estimates of range in still air. However the assumption of constant $L\/D$ and constant $V\/TSFC$ may not be too accurate in practice. To maintain constant $L\/D$ with the changing weight the aircraft would need to drift up in altitude so that a constant angle of attack was maintained. It may also be required that the aircraft change speed to maintain a constant $V\/TSFC$. So to get detailed estimates over long range cruise conditions it may be necessary to do a numerical summation over short segments where the assumptions are accurate.

Range with Headwind or Tailwind

The above calculations are based on still air conditions. If the aircraft is flying into a headwind or with a tailwind, then the distance travelled through the air is the same but the ground distance covered will change.

The energy dissipated in overcoming drag is unchanged but the effective energy output relative to the ground will be based on the relative velocity, ($V - V_w$) where $V_w$ is the velocity of the wind, positive meaning a headwind.

The energy balance becomes,

$${(V-V_w)}/{TSFC}.dW_b-DV.dt=ΔE$$

and the final range equation becomes,

$$R={(V-V_w)}/{TSFC}L/D ln({W_i/W_f)$$

Endurance

This is the total time taken during flight. It is directly related to the rate of fuel consumption. Assuming level flight with $L=W$ and $T=D$

$$dt={ds}/V={-1}/{TSFC}L/D{dW}/W={-1}/{TSFC}W/D{dW}/W={-T}/{{dW_b}\/dt}1/T.dW$$
$$dt={-1}/{dW_b\/dt} dW$$

then endurance can be found from,

$$\text"time"=∫.dt=∫_{W_i}^{W_f} {-1}/{dW_b\/dt}.dW={(W_i-W_f)}/{dW_b\/dt}$$

Optimum Range or Endurance

In order to maximise range for a given load of fuel, a balance of $V\/TSFC$ and $L\/D$ must be found. Increasing $V$ will increase range up to a point where the increasing drag will start to reduce $L\/D$ so that the range, which is the product of these two terms, again starts to reduce.

In order to maximise endurance, fuel flow rate must be reduced. For engines with roughly constant $TSFC$ this means reducing thrust by flying slowly at minimum drag speed or minimum power speed.

The optimum flight speed for maximum endurance will be quite low and may be approaching the stall speed, whereas the optimum flight speed for range will be high.

Optimum conditions for cruise flight in terms of climb, endurance and range can be found by constructing Specific Excess Power contours or Performance Envelops.