Fluid Mechanics


 
Properties of Fluids
Fluid Statics
Control Volume Analysis, Integral Methods
Applications of Integral Methods
Potential Flow Theory
Examples of Potential Flow
Dimensional Analysis
Introduction to Boundary Layers
Viscous Flow in Pipes


Non-Dimensional Numbers

Need for Non-Dimensional Numbers

Experiments are an important tools for discovery in Fluid Mechanics. Experiments are required in design and testing of vehicles such as aircraft, ships and automobiles, pumps, turbines, fans and other equipment. They are carried out in order to gain an understanding of fundamental flow phenomena such as turbulence. To give accurate results, experiments have to be planned and executed methodically. Deciding what parameters are important is fundamental to planning a correct experiment. Various scaling factors will play an important role in determining the behaviour of the flow. These factors are typically represented as non-dimensional numbers. For example, Mach Number for an experiment can determine whether the flow will have subsonic or supersonic properties. Reynolds number may be used to predict whether the flow will be smooth or turbulent. In this section non-dimensional analysis will be used to extract the important scaling factors for fluid flow.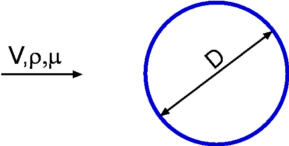


Figure 1 : Flow past a Cylinder

Consider, for example, the study of drag for the flow about a circular cylinder. What are the parameters that govern this process? From prior experimentation, it has been found that the primary parameters are

  • Freestream Speed V,
  • Diameter of the cylinder D,
  • Density of the fluid, ρ and
  • Viscosity of the fluid, μ.

In is possible to conduct a blind experiment and simply measure the influence of each of the parameters. A set of tests can be performed varying free stream speed while keeping other parameters constant. A curve can be produced of Drag vs V, keeping μ,ρ and D constant. But note that for a full set of results the same experiment has to be repeated for different values of the other parameters as well. (Fig 2.).

Then the experiment could be redone considering Drag vs ρ keeping other parameters constant. In the end an excessive number of tests would need to be carried out. If each curve requires about ten points for a good definition, it is easy to see that as many as 10,000 experiments are needed to fully cover all possibilities.

Dimensional analysis could instead be attempted before hand to detemine relationships between these parameters and hence minimise the number of experiments. This analysis technique will help determine the Non-Dimensional Numbers for the flow. The non-dimensional numbers will involve some combinations of the parameters that are dominant. In the case of drag about cylinder these are drag force, F, Density, ρ, Viscosity, μ, Diameter, D and Velocity, V.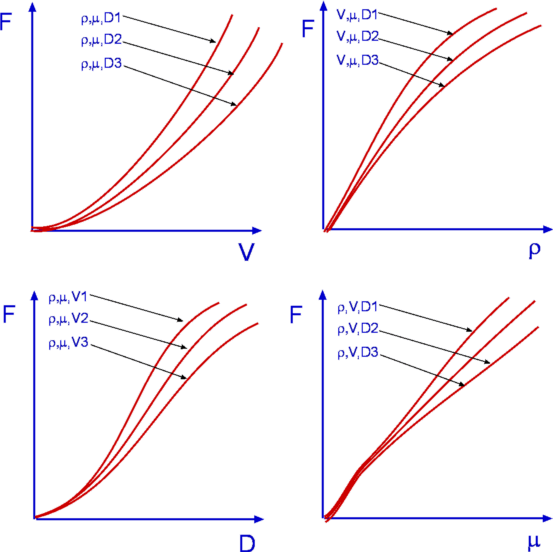



Figure 2 : Dependence of Drag on Various Parameters

During the experiments, the strategy is then to vary only these non-dimensional numbers. For example, for the drag problem, the non-dimensional numbers are the drag coefficient Cd and Reynolds number Re (see Fig 3.), which are given by

$$C_D = F/{1/2ρV^2A}\text"    ,    "R_e={ρVD}/μ$$

All full set of results describing the behaviour of the cylinder under all conditions can completed by measuring Drag coefficient while varying only the Reynolds number. While changing ρ or μ of the flow may be difficult, different Reynolds numbers can be obtained by varying both Velocity and/or Diameter.

The final result can be used to predict drag on the cylinder for any specific condition by finding drag coefficent from the graph for the specific Reynolds number of the conditions and then expanding this to a drag force.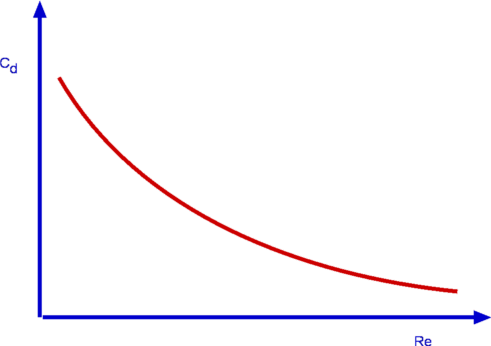



Figure 3 : Variation of Cd with Re.

Another advantage of non-dimensional numbers is that the results are independent of the units of measurement. So a person who is used to a totally different system of units can still interpret the results.

A further application of these numbers is in Similitude. Whenever a new vehicle is to be designed, initial scale model tests are normally carried out before construction of a full protptype. How do model results compare to those of the full size vehicle? Is it enough to have a geometrical similarity between the two? In practice, it requires that most of the applicable non-dimensional numbers need to be the same between model and full scale for the results to be accurate.

For many cases the Buckingham Pi Theorem helps determine appropriate non-dimensional numbers.

Buckingham Pi Theorem

Buckingham Pi Theorem relies on the identification of variables involved in a process. Further, a few of these have to be marked as "Repeating Variables". This process can be shown for the previous example of flow around a cylinder. Parameters will be, F (drag force), D (diameter of the cylinder), V (the fluid velocity), ρ (density of the fluid), μ (viscosity of the fluid). Three of these will be the Repeating Variables - V, D and ρ. The selections are made by previous expermental experience. Some general rules are however being applied. Typically the independent variables of velocity, linear dimension and density are chosen to be the Repeating Variables. In many cases, by looking at all possible variables it can sometimes be obvious what should be chosen as an independent variable and what parameters are dependent on this.

The Theorem

The Buckingham Pi Theorem enables one to determine the non-dimensional numbers governing a given process. It is often stated as,

If a physical process has "n" variables and from these "k" are Repeating Variables, then there are "n-k" independent non-dimensional numbers that can describe that process.

For the measurement of drag example, considering there are 5 variables that govern the process, n = 5. Three repeating variables have been selected, making k = 3. The theorem says that there are two non-dimensional numbers.

Application of Buckingham Pi theorem

The theorem is a very general one and by no means limited to Fluid Mechanics. It is used in diversified fields such as Botany and Social Sciences. In the fluids case, a procedure is required to obtain the non-dimensional numbers for a given flow.

Procedure:

  1. List all the variables that govern the process. These variables should be independent of each other. For example, density, gravity and specific weight should not all be chosen. Density and Specific Weight will be sufficient. For the drag measurement problem, F, D, V, ρ and μ. Thus n = 5.

  2. Mark the Repeating variables. In this case these are D, V and ρ making k = 3.

  3. Calculate how many non-dimensional numbers there are. n - k = 2. This problem has 2 non-dimensional numbers,$Π_1$ and $Π_2$.

  4. Define the non-dimensional numbers by grouping the variables into n - k groups so that each group has all the repeating variables and one non-repeating variable. Thus,

$$Π_1=Π_1(D,V,ρ,F)$$
$$Π_2=Π_2(D,V,ρ,μ)$$

Let

$$Π_1=D^aV^bρ^cF$$
$$Π_2=D^eB^fρ^gμ$$

  1. Now express each variables in terms of its dimensions. Using the MLT system according to which the variables have the following dimensions.

Variable

Dimensions

F, Force

M L / T2 or M L T-2

D, Diameter

L

V, Velocity

L/T or LT-1

ρ, Density

M/L3 or ML-3

μ, Viscosity

ML-1T-1

  1. Substituting these dimensions into equations above gives,

$$Π_1=(L)^a(LT^{-1})^b(ML^{-3})^c(MLT^{-2})$$
$$Π_2=(L)^e(LT^{-1})^f(ML^{-3})^g(ML^{-1}T^{-1})$$

or

$$Π_1=L^{(a+b-3c+1)}T^{(-b-2)}M^{(c+1)}$$
$$Π_2=L^{(e+f-3g-1)}T^{(-f-1)}M^{(g+1)}$$

  1. Noting that $Π_1$ and $Π_2$ are non-dimensional,

a + b - 3c + 1 = 0;     -b - 2 = 0,    c + 1 = 0
e + f - 3g - 1 = 0;     -f - 1 = 0,    g + 1 = 0

  1. Solving the equations yields,

a= -2,   b = -2,    c = -1
e= -1,   f = -1,    g = -1

  1. Now our non-dimensional numbers become,

$$Π_1=ρ^{-1}V^{-2}D^{-2}F\text" "=\text" "F/{ρV^2D^2}$$
$$Π_2=ρ^{-1}V^{-1}D^{-1}μ\text" "=\text" "μ/{ρVD}$$

Thus the non-dimensional numbers for the flow of interest have been obtained, namely, drag about a circular cylinder. The functional relationship between the two numbers may be expressed as

$$F/{ρV^2D^2}=\fn(μ/{ρVD})$$

But note that the form of the term $Π_2$ that has been derived is somewhat different from what was assumed at the beginning. The right hand side of the equation is actually the inverse of Reynolds number. This system only identifies the parameters and not the exact functional form between the $Π$ numbers. The functional variation between parameters must be determined by experimentation or by computation. However since the numbers are non-dimensional, the result can be written in an expected form,

$$F/{ρV^2D^2}=\fn({ρVD}/μ)$$

Important Non-Dimensional Numbers

In Fluid Mechanics there are several important non-dimensional numbers, each able to be derived using the above method. Each of these numbers turns out to be the ratio of a pair of forces. The magnitude of the number indicates the relative importance of the forces for a given flow.

Reynolds Number

Reynolds Number given by:

$$R_e={ρVL}/μ$$

is the ratio of inertial force to viscous force. A large Reynolds number indicates that for the flow intertial forces dominate the viscous forces. A large Re indicates that viscosity only has an effect in a restricted region around a body. A smaller Reynolds number means that the viscous forces are dominant in a larger region around the body.

Froude Number

Froude Number is given by:

$$F_r=(V^2/{gL})$$

and is the ratio of inertial forces to gravity forces. It is important for flows with a free surface such as the flow about ships.

Weber Number

Weber Number is defined as

$$W_e=({ρV^2L}/σ)$$

It is the ratio of inertia forces to surface tension force. If the number is small it implies that surface tension effects are important.

Pressure Coefficient

Pressure Coefficient is a non-dimensional representation of pressure and is frequently used in aerodynamic studies. It is given by

$$C_P={P-P_∞}/{1/2ρV_∞^2}$$

where P is the pressure at a point of interest and $P_∞$ is the pressure of the far-field freestream and $V_∞$ is the freestream speed.

Drag and Lift Coefficients

These are defined as

$$C_D=D/{1/2ρV^2A}\text"    ,    "C_L=L/{1/2ρV^2A}$$

where D and L are drag and lift forces respectively.

Some of the common non-dimensional numbers in Fluid Mechanics have been listed in Table 1.

Table 1. Important Non-Dimensional Numbers.

Non-Dimensional Number

Definition

Significance

Application

Reynolds Number, Re

${ρVL}/μ$

${\text"Inertial Forces"}/{\text"Viscous Forces"}$

All Fluid Dynamics

Mach Number, M

$V/a$

${\text"Flow Speed"}/{\text"Speed of Sound"}$

Compressible Flow

Froude Number, Fr

$V^2/{gl}$

${\text"Inertial Forces"}/{\text"Gravity Force"}$

Free Surface Flows

Prandtl Number, Pr

${μC_p}/γ$

${\text"Viscous Dissipation"}/{\text"Heat Conduction"}$

Heat Transfer

Ratio of Specific Heats, γ

$C_p/C_v$

${\text"Enthalpy"}/{\text"Internal Energy"}$

Compressible Flow

Roughness Ratio

$e/L$

${\text"Height of Roughness"}/{\text"Length of Body"}$

Turbulent Flows

Pressure Coefficient, CP

${P-P_∞}/{1/2ρV^2}$

${\text"Static Pressure"}/{\text"Dynamics Pressure"}$

Aerodynamics, Hydrodynamics

Force Coefficient, CX

$X/{1/2ρV^2A}$

${\text"Force"}/{\text"Dynamic Pressure"×\text"Area"}$

Aerodynamics, Hydrodynamics

Firction Coefficient, Cf

$τ_{wall}/{1/2ρV^2}$

${\text"Wall Shear Stress"}/{\text"Dynamics Pressure"}$

Boundary Layer Flow

Similitude

Similitude is an important application of non-dimensional numbers. Is it possible to get accurate results from a scale model test? Suppose a new aircraft is to be manufactured and wind tunnel testing of a model is going to be carried out to estimate likely performance. What should be the flow conditions for such a test to ensure the laboratory results are applicable to the full-scale situation. Three types of similarities are required between the model and the full-scale prototype. These are Geometric Similarity, Kinematic Similarity and Dynamic Similarity.

Geometrical Similarity

It is an obvious requirement that the corresponding lengths between the model and the prototype bear the same ratio as shown in Fig 4.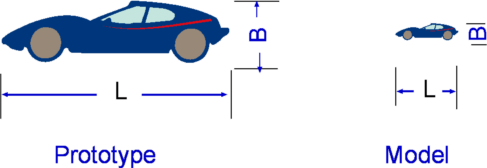



Figure 4 : Geometric Similarity
$$(L/B)_{model}=(L/B)_{prototype}\text"    ,    "(t/B)_{model}=(t/B)_{prototype}\text"    ,    etc."$$

Kinematic Similarity

This similarity requires that the length (L) and time (t) scales be similar between the model and the prototype implying that velocities at corresponding points be similar as shown in Fig 5. Under this similarity streamline patterns for the flow over the model and the prototype will be similar. Obviously, kinematic similarity includes geometrical similarity.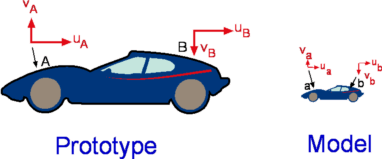


Figure 5.5 : Kinematic Similarity
$$(v_a/u_a)_{model}=(v_A/u_A)_{prototype}\text"    ,    "(v_b/u_b)_{model}=(v_B/u_B)_{prototype}\text"    ,    etc."$$

Dynamic Similarity

Dynamic Similarity exists between the model and the prototype when forces at corresponding points are similar (Fig. 6.).

$$({Fa}_v/{Fa}_h)_{model}=({FA}_v/{FA}_h)_{prototype}\text"    ,    "({Fb}_v/{Fb}_h)_{model}=({FB}_v/{FB}_h)_{prototype}\text"    ,    etc."$$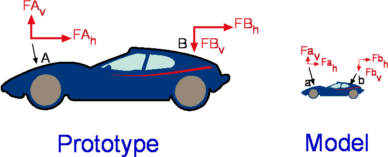

Figure 6 : Dynamic Similarity

Of the three similarities, the dynamic similarity is the most restrictive.

The Dimensional Analysis process indicates that to achieve dynamic similarity then all the non-dimensional numbers relevant to the flow must be preserved between the model and the prototype, i.e.,

$$Π_{1(model)}=Π_{1(prototype)}\text"    ,    "Π_{2(model)}=Π_{2(prototype)}\text"    ,    etc."$$

However, in common practice, this is something not easy to achieve. For example, in the field of aerodynamics, in order to obtain total similitude between model and prototype it is required that Reynolds Number and Mach Number should be the same between the model and the prototype. Considering that the inflight Reynolds numbers of a large aircraft is around 108 it appears that small scale models would need to be run at a much higher speed than the prototype. This would mean that Mach Number matching is not possible. However, it turns out that at lower speeds (Mach Number 0.3 and below) it is the Reynolds Numbers that are important and it is simply enough to preserve Reynolds number alone. At higher speeds where compressibility is important only Mach Number need be preserved.