Gas Dynamics &
|
Equations of Motion for a Compressible FlowIn this section the equations of motion for a compressible flow are derived. For an incompressible flow velocity is calculated from continuity or momentum equation. Pressure is obtained through the Bernoulli Equation. This simple approach is not possible for a compressible flow where temperature is not a constant. The energy equation needs to be solved in addition to the continuity and momentum equations. The latter equations have previously been derived for incompressible flows in the section on Fluid Mechanics. In this case, they will be applied considering that there will be changes in density. The Integral Approach is used based on a control volume as show below. Equations are derived under the following assumptions.
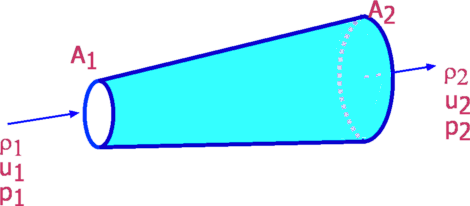 Figure 8: Control Volume for a Compressible Flow Continuity EquationFor a steady flow, the mass flow rates at entry (1) and exit (2) of the control volume must be equal. Hence, $$ρ_1u_1A_1=ρ_2u_2A_2$$ Written in a differential form the above equation becomes,
$$d/{dx}(ρuA) =0$$ Momentum EquationThe derivation of Momentum Equation closely follows that for incompressible flows. Basically, it equates net force on the control volume to the rate of change of momentum of the gas entering or exiting the control volume. Defining $P_m$ as the average pressure between the entry (1) and exit (2),(see Fig. 8), then for a steady flow, $$P_1A_1+(ρ_1u_1A_1)u_1+P_m(A_2-A_1)=P_2A_2+(ρ_2u_2A_2)u_2$$ For a steady flow through a duct of constant area the momentum equation assumes a simple form, $$P_1+ρ_1u_1^2=P_2+ρ_2u_2^2$$ It should be noted that the above equations can be applied even for the cases where frictional or viscous effects occur between locations (1) and (2). But it is necessary that these effects be absent at (1) and (2). Energy EquationFrom the first law of Thermodynamics, for a unit mass, $$q + \text"work done" = \text"increase in energy"$$ where $q$ is the heat added. Work done is given by $$dw = P_1v_1 - P_2v_2$$ Considering only internal and kinetic energies. Accordingly, $$\text"Change of energy" = (e_2+1/2u_2^2)-(e_1+1/2u_1^2)$$ where $e$ is specific internal energy and $u$ is flow velocity Substituting produces the energy equation for a gas flow as, $$q+P_1v_1-P_2v_2=(e_2+1/2u_2^2)-(e_1+1/2u_1^2)$$ Noting that enthalpy, $h= e + P.v$, then $$q=h_2-h_1+1/2u_2^2-1/2u_1^2$$ Considering an adiabatic process, $q = 0$, then, $$h_2+1/2u_2^2=h_1+1/2u_1^2$$ This equation demands that the states (1) and (2) be in equilibrium, but does allow non-equilibrium conditions between (1) and (2). If the flow is such that equilibrium exists all along the path from (1) to (2) then, at any location along 1-2, $$h+1/2u^2 = \text"constant"$$ Differentiating the above equation, $$dh+udu=0$$ For a thermally perfect gas i.e., enthalpy, $h$ depends only on temperature, $T$ ($h=c_pT$) the above equation becomes, $$c_pdT+udu=0$$ Further, for a calorically perfect gas, i.e., $c_p$ is constant, then, $$c_pT+1/2u^2=\text"constant"$$ Stagnation ConditionsThe "constant" on the RHS of the above equation can be determined by looking at the flow at either stagnation conditions, as was the case for incompresible flow, or at sonic (M=1) conditions. Constant based on Stagnation ConditionsStagnation conditions are reached when the flow is brought to rest,i.e., $u=0$. Temperature, pressure, density, entropy and enthalpy become equal to "Stagnation Temperature" , $T_0$, "Stagnation Pressure", $P_0$ , "Stagnation Density", $ρ_0$ "Stagnation Entropy", $s_0$ and "Stagnation Enthalpy, $h_0$. These are also known as "Total" conditions. This is in contrast to incompressible flows where only the Stagnation Pressure is considered. The previous equation can be re-written as, $$h+1/2u^2=h_0$$ Note that $h = c_pT$ for a calorically perfect gas, hence, $$c_pT+1/2u^2=c_pT_0$$ The constant arrived at is thus $h_0$ or $c_pT_0$. It is to be noted that there does not have to be a stagnation point in a flow in order to use the above equations. Stagnation or Total conditions are only reference conditions. There is only one stagnation condition for a given flow, although in fact this only is true for isentropic flows. In a non-isentropic flow different locations can have different stagnation conditions depending on the energy or heat supply to the different points in the flow. In an adiabatic flow (a flow where heat is not added or taken away) the stagnation or total temperature, $T_0$ does not change. This is true even in presence of shock waves as described later. However the total pressure $P_0$ can change from point to point. Considering the control volume shown in Fig. 8, as long as the flow is adiabatic, then, $$(T_0)_1=(T_0)_2$$ To predict the conditions for total (stagnation) pressure, the Second Law of Thermodynamics, is used, $$(s_0)_2-(s_0)_1≥0$$ For a perfect gas the above equation becomes, $$R\ln({(P_0)_1}/{(P_0)_2})+c_p({(T_0)_2}/{(T_0)_1})≥0$$ Since $(T_0)_1=(T_0)_2$ $${(P_0)_1}/{(P_0)_2}≥0$$ "Equals" sign applies when the flow is isentropic and "greater than " sign applies for any non-isentropic flow. Thus for any natural process involving dissipation, total pressure drops. It is preserved for an isentropic flow. An example of a non-isentropic flow is that of a shock wave. Across a shock wave there is a reduction of total pressure. Area-Velocity RelationIn incompressible flow velocity changes inversely with area changes - as the area offered to the flow increases, velocity decreases and vice versa. But a compressible flow at supersonic speeds reverses this relationship due to the effect of the speed of sound in the gas. The Continuity equation is, $${∂ρ}/ρ+{du}/u+{dA}/A=0$$ Considering also the Euler Equation (derived before for incompressible flows) $$u.du + {dP}/ρ=0$$ Rewriting the equation, $$u.du=-{dP}/ρ=-{dP}/{dρ}{dρ}/ρ=-a^2{dρ}/ρ$$ brings in the speed of sound, given by $a=√{dP\/dρ}$. By introducing Mach Number, $M = u\/a$ the above equation becomes, $${dρ}/ρ=-M^2{du}/u$$ Upon substituting this in the continuity equation, $${du}/u=-{{dA}/A}/{1-M^2}$$ 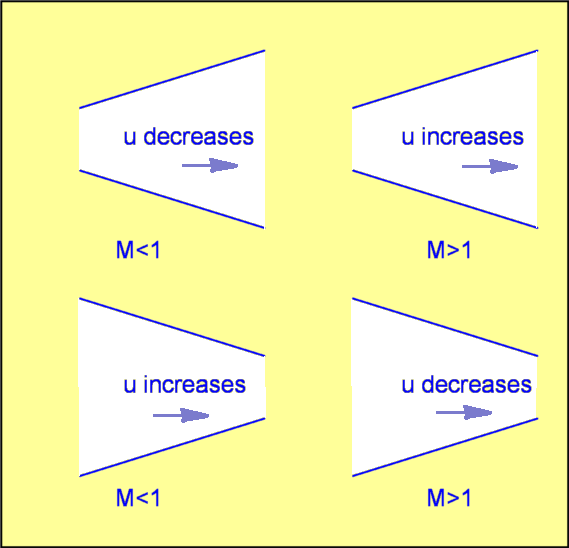 Figure 9 : Response of Subsonic and Supersonic Flows to Area Changes Applying this equation produces the effects shown in Fig. 9
|