Gas Dynamics &
Supersonic Flow

Wave Propagation

Information regarding flow properties propogates via waves. These waves travel at the local speed of sound. There is a noticable contrast between incompressible and compressible flows. For an incompressible fluid the speed of sound is infinite (Mach number is zero). Consequently, information in the form of pressure, density and velocity changes is conveyed to all parts of the flow instantaneously. The flow therefore changes instantaneously due to an intrduced disturbance. The stream lines of an incompressible flow are continuous and the flow changes smoothly to accommodate the presence of a body placed in the flow. Changes occur far upstream of the body.This may not happen in compressible flows. In a compressible medium any disturbance travels only at finite speeds. Signals generated at a point in the flow take a finite time to reach other parts of the flow. The smooth streamline pattern noticed for incompressible flow may now be absent.

In this section an expression for the speed of sound is derived. The difference between supersonic flow and subsonic flow responses to a disturbance due to the presence of anobstacle in the flow will be investigated. Shock waves may be formed in compressible flows.

Speed of Sound

Consider a sound wave propagating to the right as shown (Fig. 11) with a speed $a$. The medium to the right is at rest and has pressure, density and temperature $P, ρ, T$ respectively. As a consequence of wave motion the medium gets compressed and the gas is set to motion. Let the speed of gas behind the wave be $du$. Pressure, Density and temperature will now be $P+dP, ρ+dρ, T+dT$ respectively.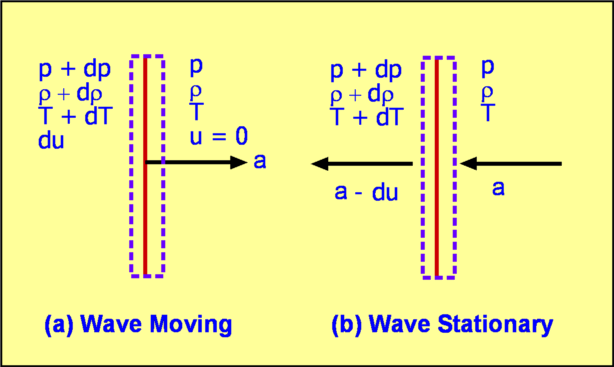

Figure 11 : Speed of Sound

For analysis it is easier to make the wave stationary, ie. choose a frame of reference that is moving with the wave. Accordingly, an equal and opposite speed $a$ (equal to the wave speed) is superimposed. This is shown in part (b) of Fig. 11.

Applying the equations of mass and momentum to the control volume shown gives,

Simplifying the continuity equation and ignoring the small products such as $du.dρ$ gives,

Replacing the term $(ρ+dρ)(a-du)$ in the momentum equation, leads to

which simplifies to

Combining Eqns.,

If the propagation of a sound wave is considered to be an isentropic process, the above equation becomes,

For a perfect gas the above expression reduces to,

Any change in flow conditions is transmitted to other parts of the flow by means of waves travelling at the local speed of sound. The ratio of flow speed to the speed of sound , called Mach Number, is an important parameter for a given flow. As an equation,

Mach Number is a measure of the relative importance of compressibility effects for a given flow.

Propagation of a Source of Sound

A point source of sound will produce different disturbances in the flow if it moves at different speeds.

Stationary Source

A stationary source emits a sound waves at regular intervals eg. every second. The waves travel in the form of a circle with the centre at the location of the source as shown in Fig. 12 (a). After 3 seconds there will be three concentric circles as shown. The effect of the sound source is felt at a point as the edge of a circle reaches that point.

Source moving at Subsonic Speeds

If the source moves to the left at half the speed of sound, i.e., $M = 0.5$ then the source will be at different positions as the waves are released as shown. In this case the sound travels faster than the particle, but the particle moves so that the origin of each circel is different and the waves produced are closer together on the side toward which the particle is moving. This gives rise to the Doppler effect where frequency of the waves to a stationary observer appears different if they are infront of the moving object or behind.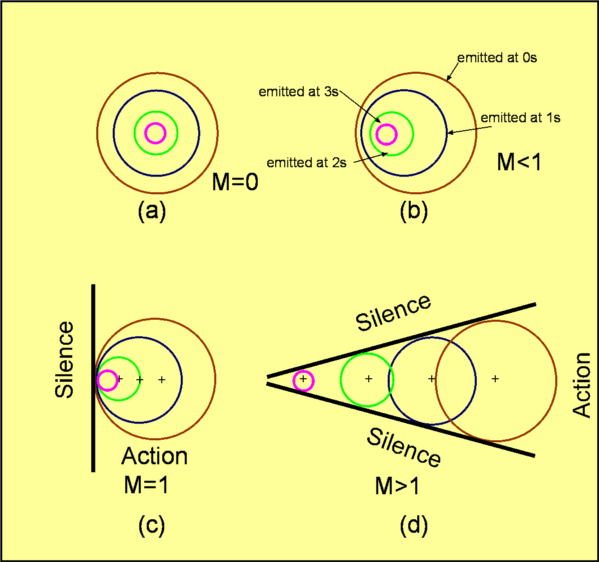

Figure 12: Propagation of a Source of Sound at different speeds

Source moving at the Speed of Sound

In the situation where the source moves at the speed of sound, i.e., Fig 12(c) then sound waves travel with the particle speed and do not "outrun" it. Consequently, the circles representing wave motion touch each other as shown. A line which is tangential to each of these circles can be drawn such that any effect of the sound wave is felt only to the right of this line. In the region to the left of the line no effect of the source of the sources is detected until the particle reaches that point. These regions are designated "Zone of Action" and "Zone of Silence" respectively.

Source moving at Supersonic Speeds

The situation becomes dramatic when the source moves at speeds greater than the speed of sound. The boundary between the Zone of Silence and the Zone of Action is not a single straight line, but two lines meeting at the current position of the source. In addition, the Zone of Action is now a more restricted region. A stationary observer does not hear any sound till they are within the Zone of Action. This is a common experience when a supersonic aircraft flies past. An observer on the ground first sees the aircraft but hears nothing. They have to wait till the aircraft flies past and "immerses" them in the Zone of Action. In case of a subsonic aircraft, the observer hears the sound as the aircraft approaches.

The boundary between the two zones is called a Shock Wave It is a straight line where the sound disturbances have coalesed and where there will then be a step change in gas properties. If the shock wave is relatively weak producing only minimal changes in properties, then it is called a Mach Wave The half angle of the wedge produced at supersonic speeds by a weak wave is called the Mach Angle, $μ$.

Mach Angle is a function of the Mach Number of the flow and is in this sense a property of the flow. Values are listed in Tables at the end of this section.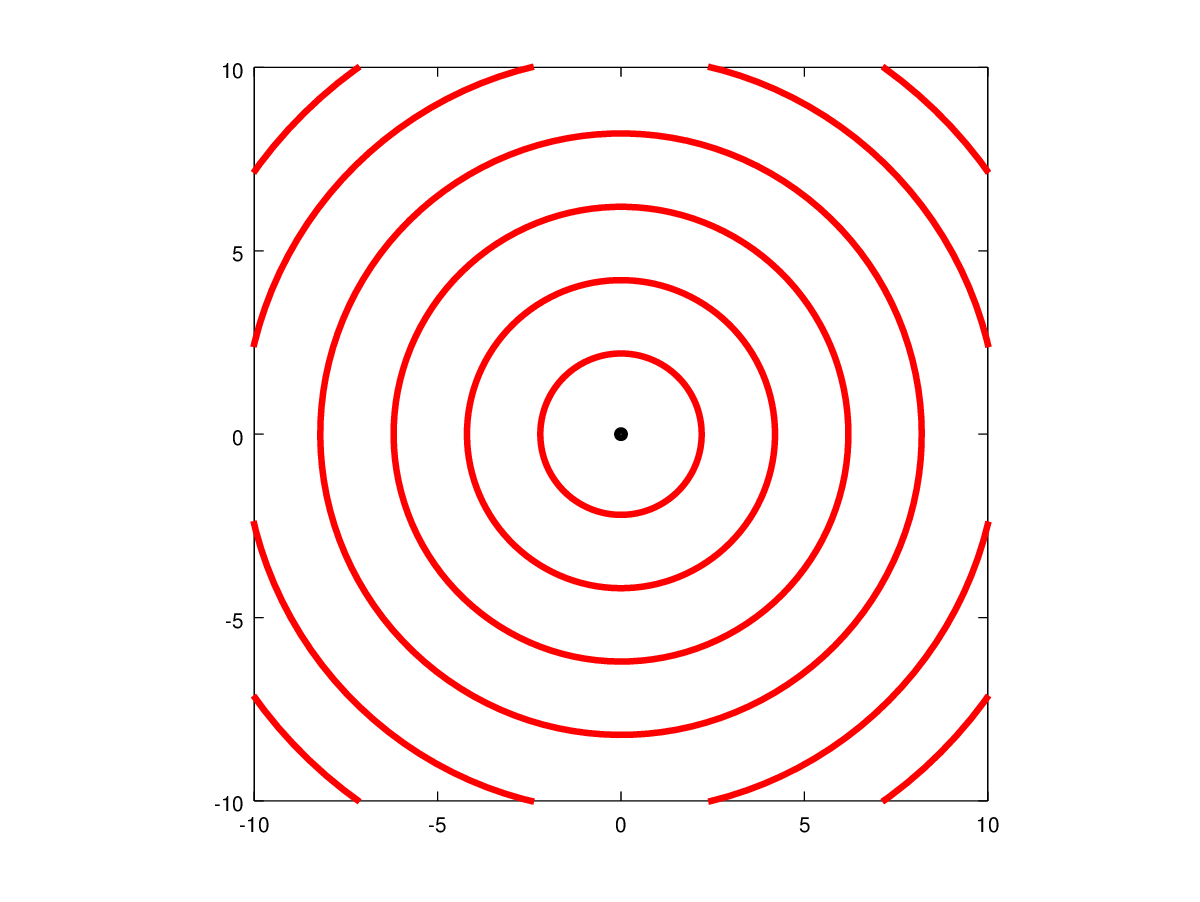

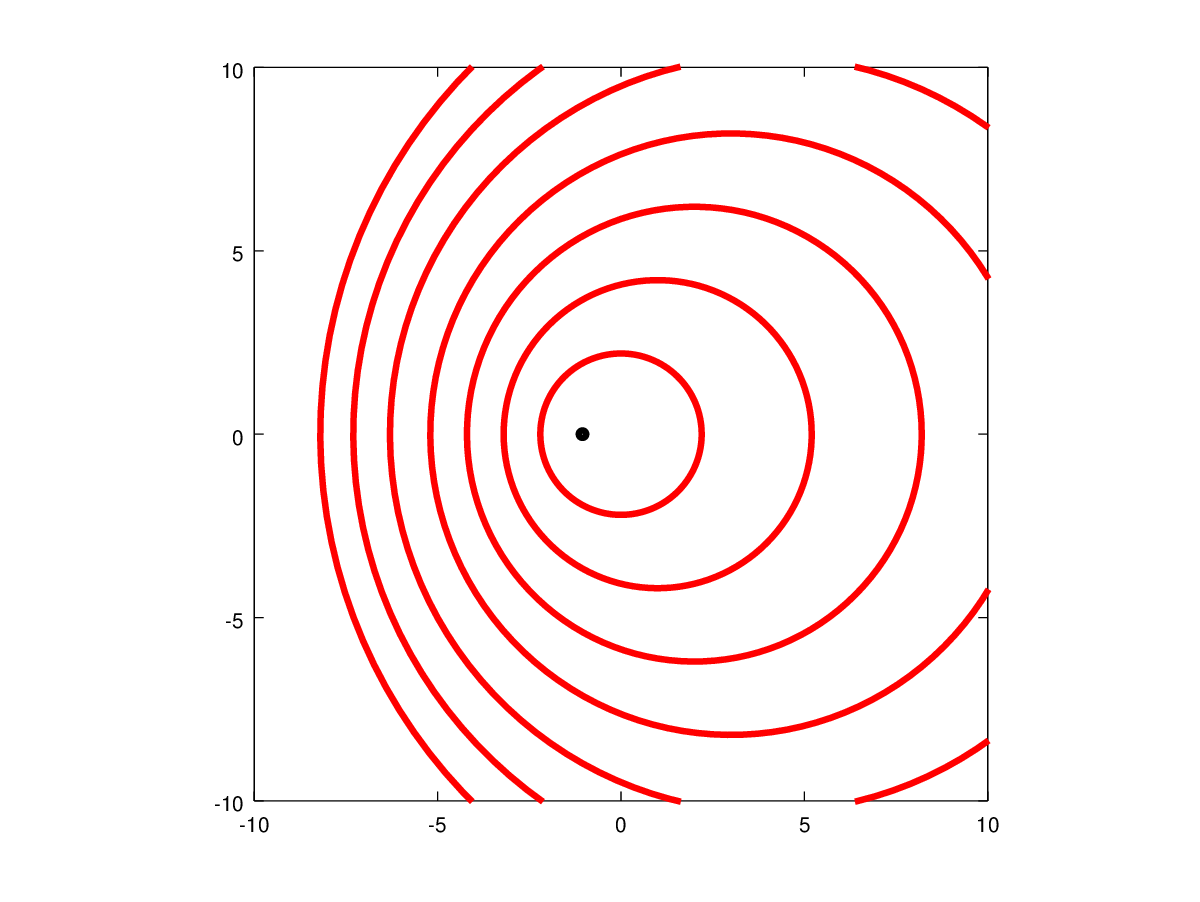
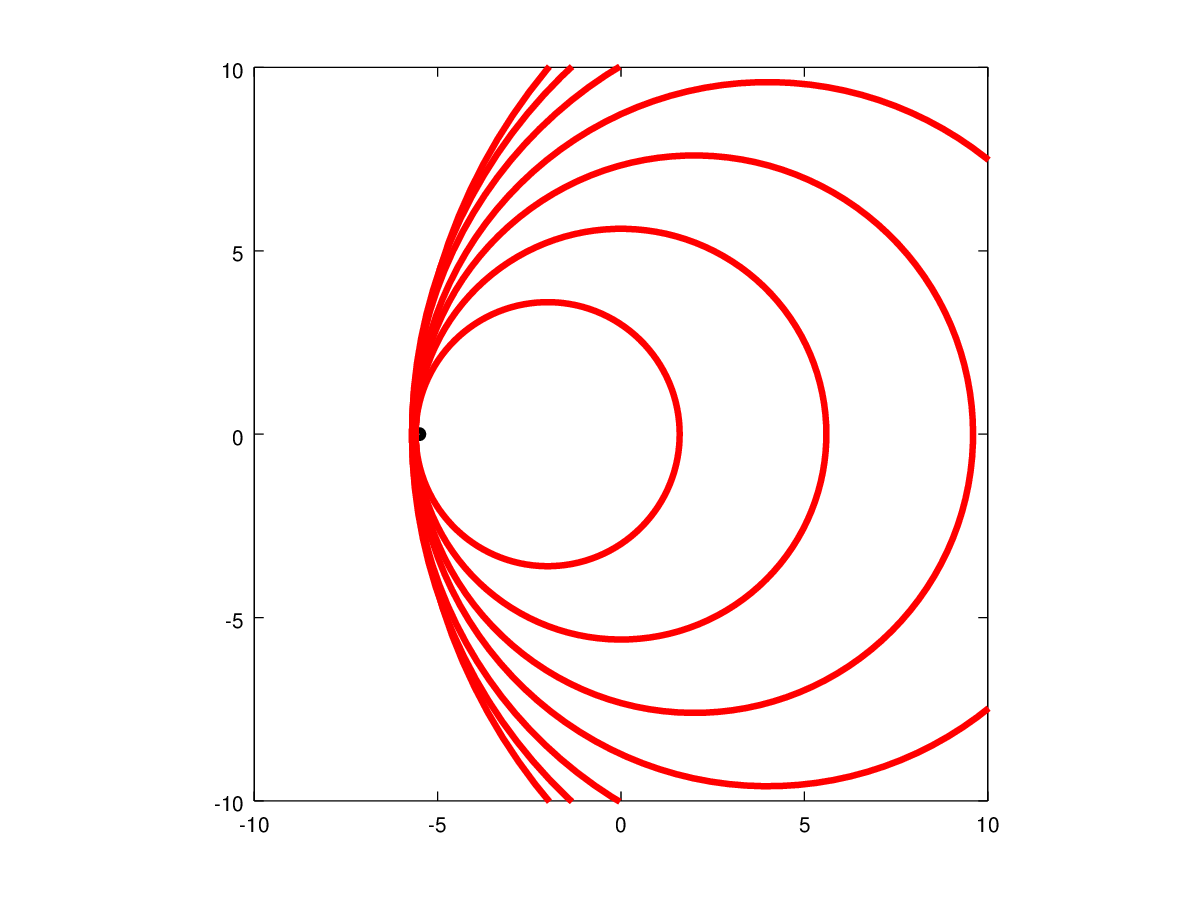
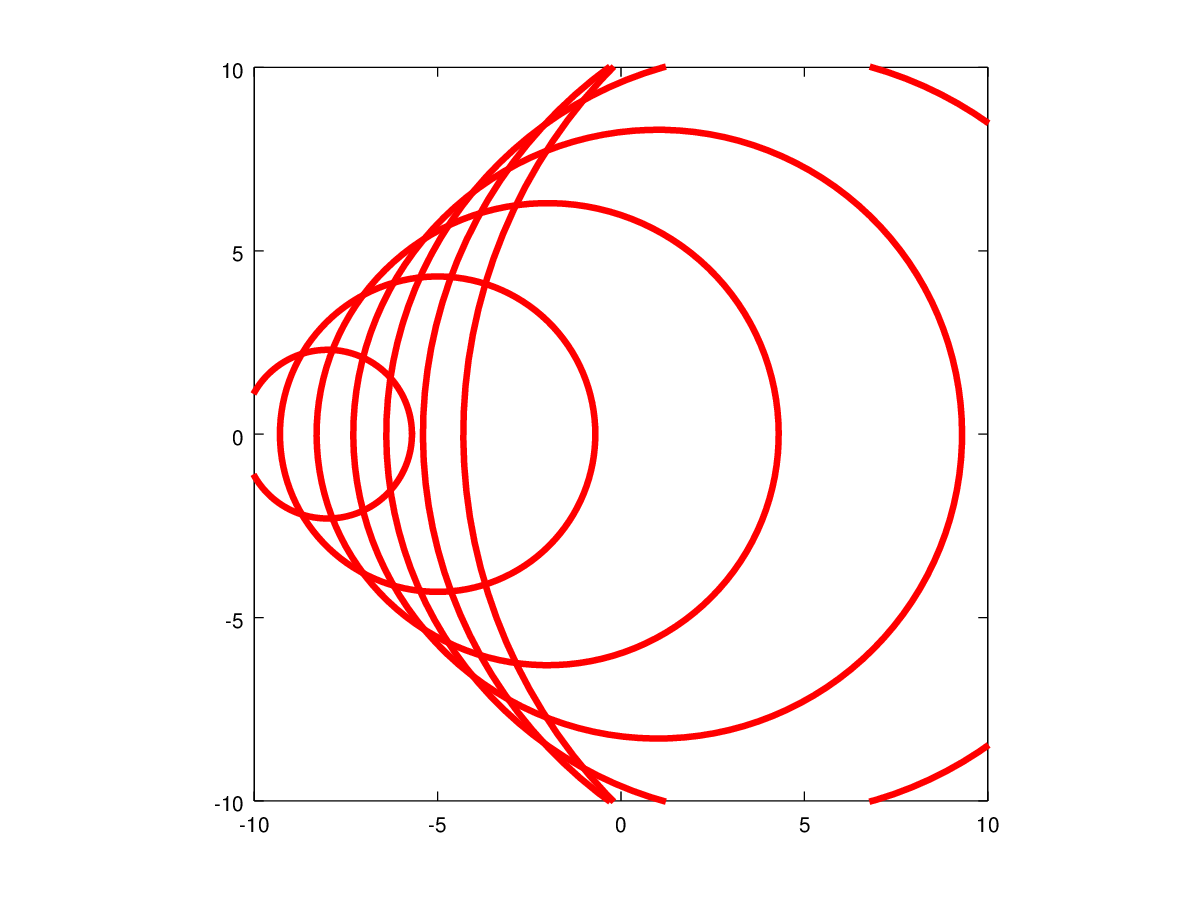Visualisations of Wave Propogation. Stationary Object : Moving-Subsonic : Moving-Sonic : Moving-Supersonic

Response of Subsonic and Supersonic Flows to an Obstacle

If an obstacle placed in subsonic or supersonic then its presence produces disturbances moving at the speed of sound and will have different effects upon the flow depending on Mach Number.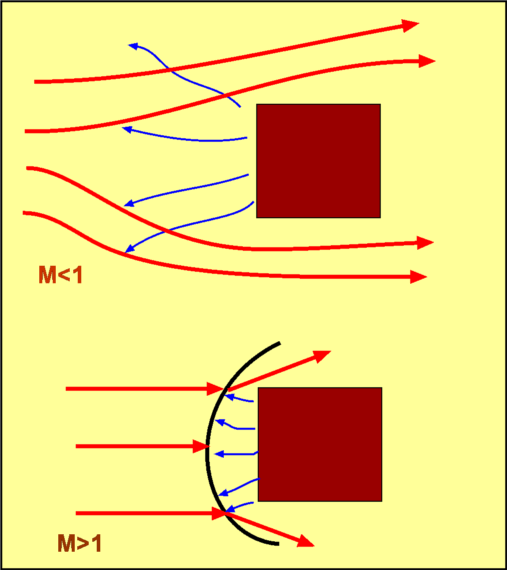

Figure 13 : A Body placed in Subsonic and Supersonic Flows

Subsonic Flow

If a body is placed in a subsonic stream, any disturbances propagate at the speed of sound. Since the incoming flow is slower than sound, these disturbances can propagate upstream. As they propagate upstream, they modify the incoming flow. Consequently the flow adjusts itself to the presence of the body sufficiently upstream and flows past the body smoothly. This is also what happens with incompressible flows where the speed of sound is effectively infinite.

Supersonic Flow

With a supersonic flow disturbances are formed as a result of flow interacting with the body. But now they cannot propagate upstream because the incoming flow is faster. Any signal that tries to go upstream is pushed back towards the body. These signals, unable to go upstream, pile up closed to the body (Fig. 13). The incoming flow is therefore not "warned" of the presence of the body. It flows as if the body is absent until it encounters the region where the disturbances have builtup up. Then the flow suddenly modifies itself to accommodate the presence of the body. This marks a sharp difference between subsonic and supersonic flows.

The example indicates that in a supersonic flow disturbances cannot propagate upstream. This technically stated as "In a Supersonic flow there is no upstream influence". Further the region where the disturbances have "piled up" is a Shock Wave. These are regions of infinitesimally small thickness across which flow properties such as pressure, density and temperature can sometimes jump, orders of magnitude, depending upon the Mach Number of the flow.

Shock Waves

The analysis of shock waves for 1-D flow are considered in this section, In a later section this will be expanded to cover two-dimensional flows.

Formation of a Shock Wave

A piston-cylinder arrangement is shown in Fig. 14. A gas is at rest in front of the piston with pressure, density and temperature given by $P, ρ$ and $T$. The piston will start moving at time, $t=0$. This start-up produces disturbances, compression waves in the flow. A weak wave is emitted (a in the figure). The wave moves to right at a speed $a$ , i.e., the speed of sound. The wave as it propagates sets the gas into motion. Accordingly behind the wave is a medium which is slightly compressed. Its properties are given by $P+dP_1, ρ+dρ_1$ and $T+dT_1$.

If the piston is given an increase in speed (b in the figure), then another disturbance wave is generated. Its speed, however is not $a$ , but is $a + da_1$. This wave has a higher speed because it is generated in a medium of higher temperature. The second wave chasing the first will eventually catchup and merge with the first one to produce a stronger wave. The pressure jump across the stronger wave is not $dP_1$ but is $dP_1+dP_2$. This phenomenon where the waves merge is called Coalescence.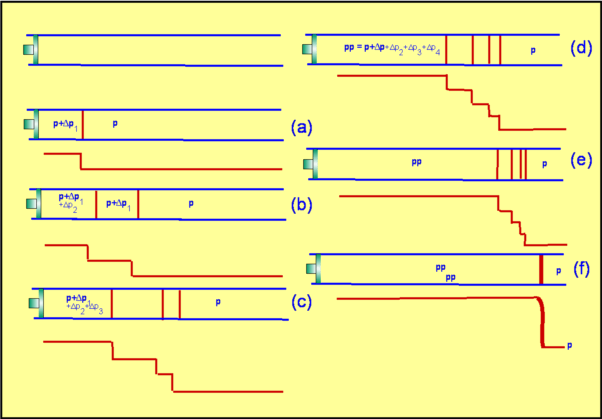

Figure 14 : Formation of a Shock Wave

If the situation is one where the piston is accelerated over a period of time (a,b,c and d in Fig. 14) or the piston is pushed continuously, then there will be a train of waves where each wave is stronger and faster than the one before. Very soon these waves coalesce into a strong wave with a measurable pressure and temperature jump across it. This is a Shock Wave.

Normal Shock Waves

The formation of shock waves can occur in two different situations.

1. when a supersonic flow negotiates an obstacle and
2. when a piston is pushed inside a cylinder.

In order to analyse a shock and see how flow properties change, it is easiest to choose a stationary frame of reference which moves with the wave. This is applicable to both situations in 1-D flow. The shock wave is assumed to be normal to the flow and across it properties can jump by big magnitudes. A normal shock in a flow with a Mach number of $3$ will have a pressure which jumps $10.333$ times across it. This jump occurs in a distance of about $10^{-6}$ cm. The shock thickness is so small that for all practical purposes it is a discontinuity.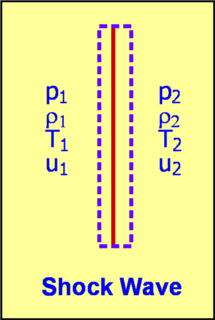

Figure 15 : Shock Wave

Consider a shock wave as shown, across which pressure, density, temperature, velocity,etc, jump from $P_1, ρ_1, T_1, u_$ ... to $P_2, ρ_2, T_2, u_2$ . If a control volume is put around it, assuming no change in area between 1 and 2 then the governing equations are

Noting that the term $ρu^2$ in the momentum equation is

The momentum equation now becomes,

The energy equation requires that total enthalpy, $h_0=h+u^2\/2$ is constant across the shock. Accordingly,

which for a perfect gas becomes, $T_{01}=T_{02}$, substituting gives,

The expressions derived are for temperature and pressure ratio across a shock wave. Density ratio follows from the perfect gas equation,

Substituting for $ρu$ as $P/{RT}M√{γRT}$ the continuity equation becomes,

Substituting for pressure ratio,

Substituting for temperature ratio,

This equation connects Mach Numbers across a normal shock. The Mach number downstream of the shock, $M_2$ is a function of Mach Number upstream of the shock, $M_1$ and ratio of specific heats, $γ$.

The equation has two solutions given by,

Any imaginary solutions for these Eqns are ruled out. One of the possible solutions, $M_1 = M_2$ is trivial telling that there is only an extremely weak shock.

Once the relationship between $M_2$ and $M_1$ has been found, the relationships that connect pressure, density, and other variables across the shock can be derived. This is done by substituting for $M_2$ in the equations derived above.

The final form of the equations are,

Considering now the "Total" properties,

Change in entropy across the shock is given by

and

which in terms of $M_1$ alone becomes,

Tables and scripts at the end of this section have the values of the ratios of pressure, density, temperature, Mach Numbers etc tabulated for different inlet Mach Numbers, i.e. $M_1$.

Important Characteristics of a Normal Shock

Mach numbers are plotted in Fig. 16 to reveal an important property of normal shocks. It can be seen from the plot that -

• If $M_1 > 1$ then $ M_2 < 1$ , i.e, if the incoming flow is supersonic , the outgoing flow is subsonic.
• If $M_1 < 1$ then $M_2 > 1$ , i.e, if the incoming flow is subsonic, the outgoing flow is supersonic.

It appears that both the solutions are mathematically possible. But if the entropy change of the situation is investigated (Fig 16(b)) then a fundamental rule of thermodynamics is violated by one of the solutions.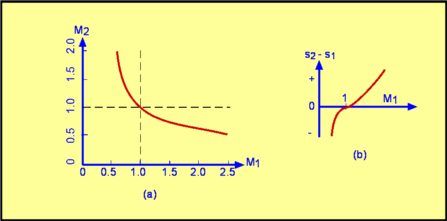

Figure 16 : Downstream Mach Number M₂ and Entropy rise across a shock.

It comes out that if $M_1 < 1$ then we have a decrease in entropy across the shock, which is a violation of the second law and therefore a physical impossibility. This solution would give a shock which tries to expand a flow and decrease pressure. Hence, it is clear that expansion shocks are ruled out.

If $M_1 > 1$ there is an increase in entropy, which is physically possible. This is a compressive shock across which pressure increases. So the traffic rules for compressible flows are such that shocks are always compressive, incoming flow is always supersonic and the outgoing flow is always subsonic.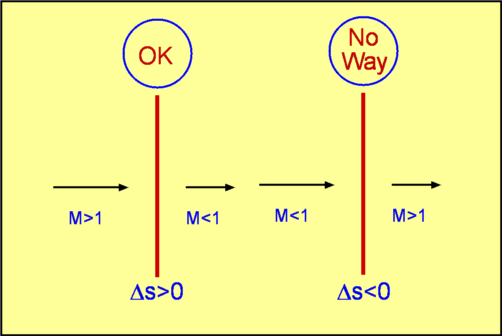

Figure 17: Traffic Rules for Compressible Flow.