Gas Dynamics &
|
1-D Isentropic Flow EquationsFor an isentropic flow, all the static properties such as $P, ρ, T$ and $s$ when expressed as a ratio the flow stagnation values become functions of Mach Number, $M$ and $γ$ alone. From the energy equation, $$c_pT+1/2u^2=c_pT_0$$ Eliminating $T$ using the equation for speed of sound (for proof see section below ), $a^2=γRT$, then $${γR}/{(γ-1)}a^2/{γR}+1/2u^2={γR}/{(γ-1)}a_0^2/{γR}$$ where a0 is the stagnation speed of sound. The above equation simplifies to $$a^2/{γ-1}+1/2u^2=a_0^2/{γ-1}$$ Multiplying throughout by $(γ-1)\/a^2$ yields, $$a_o^2/a^2=T_0/T=1+{γ-1}/2M^2$$ This is the first relationship which connects temperature ratio with Mach Number. Assuming isentropy and using the relation, $P = \text"constant" × ρ^γ$ , expressions can be derived for pressure and density,
$$P_0/P=(1+{γ-1}/2M^2)^{γ/{γ-1}}$$ These relations prove very useful in calculating isentropic flows. Once Mach Number is known it is easy to calculate pressure, density and temperature as ratios of their stagnation values. These are tabulated as functions of Mach number in tables at the end of this section along with calculation scripts.
Sonic Point as ReferenceThe preceding relations were arrived at with stagnation point as the reference. It is also possible to choose the sonic point, the location where $M = 1$ as the reference. At this point $u = u^\text"*"$ and $a = a^\text"*"$ . Since $M = 1$ , then $u^\text"*" = a^\text"*"$. As a consequence the energy equation, becomes $$u^2/2+a^2/{γ-1}=u^{\text"*2"}/2+a^{\text"*2"}/{γ-1}=1/2{γ+1}/{γ-1}a^{\text"*2"}$$ Comparing with the temperature version of the energy equation then, $$a^{\text"*2"}/a_0^2=2/{γ+1}=T^{\text"*"}/T_0$$ As a result for air with $γ = 1.4$, the values are
$$T^{\text"*"}/T_0=0.833\text" , "a^{\text"*"}/a_0=0.913$$ It should be noted that a sonic point need not be present in the flow for the above equations to be applicable. Mass Flow RateAn equation for mass flow rate can be determined in terms of Mach Number of flow. The area in an isentropic flow where the Mach Number becomes 1, is $A^\text"*"$. This is typically the throat location in a converging-diverging flow. The mass flow rate is given by, $$m↖{.}=ρuA$$ For an isentropic flow $$m↖{.}=ρuA=ρ^{\text"*"}u^{\text"*"}A^{\text"*"}$$ By noting that when $M=1, u^\text"*"=a^\text"*"$ $$A/A^{\text"*"}={ρ^{\text"*"}/ρa^{\text"*"}/u=ρ^{\text"*"}/ρ_0 ρ_0/ρ a^{\text"*"}/u$$ Substituting for terms such as $ρ^\text"*"/ρ, ρ/ρ_0, a^\text"*"$, etc. and simplifying, then, $$(A/A^{\text"*"})^2=1/M^2[2/{γ+1}(1+{γ-1}/2M^2)]^{{γ+1}/{γ-1}}$$ This is a very useful result. It connects the local area and local Mach Number. Tables at the end of this section list this function, $A\/A^\text"*"$ as a function of Mach Number. It helps determine changes in Mach Number as area changes. 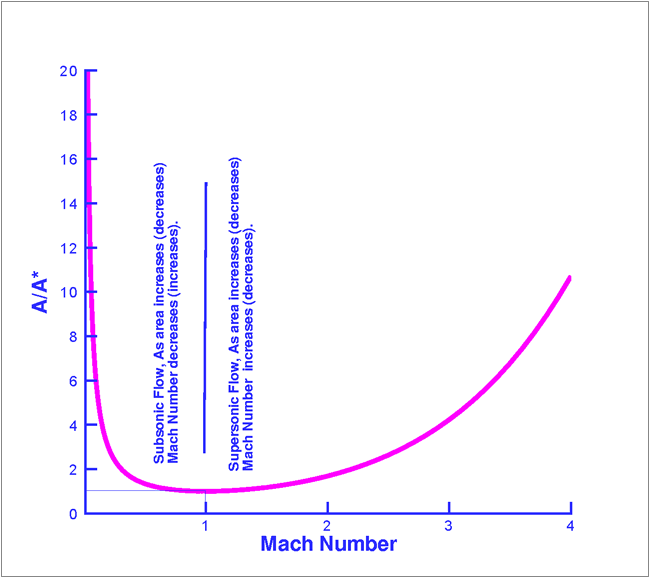 Figure 10 : Mach Number as a function of area. Fig 10 shows the area function $A\/A^\text"*"$ plotted as a function of Mach Number. For subsonic flows Mach Number increases as the area decreases and it decreases as the area increases. While with supersonic flows, Mach Number decreases as area decreases and it increases as area increases. Equations of Motion in absence of Area ChangesThe equations that we have derived for mass, momentum and energy can be used for cases where there is no area change,
$$ρ_1u_1=ρ_2u_2\text" , "P_1+ρ_1u_1^2=P_2+ρ_2u_2^2$$ |