Gas Dynamics &
|
Prandtl-Meyer ExpansionIn this section the expansion of a flow is considered. A supersonic flow negotiating a convex corner undergoes expansion. As Expansion Shocks are not possible for steady flow, then expansions will be produced by a series on Mach waves. The expansion will be an isentropic process. 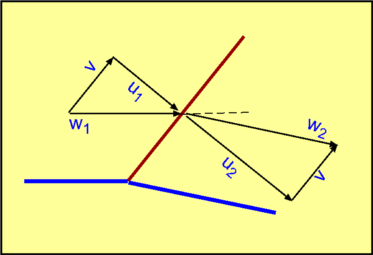 Figure 33: Flow expansion through a shock? The waves may be centered at a convex corner or spread out as in the case of a convex surface. The Mach Waves are divergent in both the cases. A centered wave is called a Prandtl-Meyer Expansion fan. 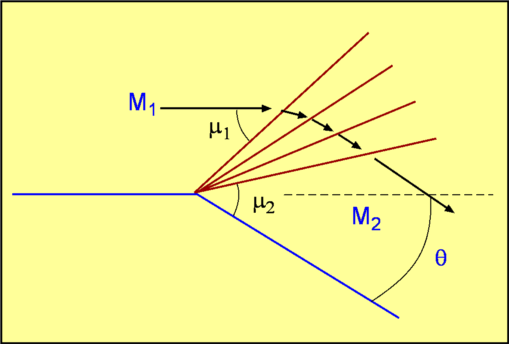 Figure 34 : Prandtl-Meyer Expansion A Prandtl-Meyer fan is shown in Fig. 34, through which a flow expands from a Mach Number, $M_1$ to $M_2$. The leading wave is inclined to the flow at an angle $μ_1=\sin^{-1}(1\/M_1)$ and the expansion terminates in a wave inclined at an angle, $μ_2=\sin^{-1}(1\/M_2)$ . An expression connecting the flow turning angle $θ$ and the change in Mach Number can be found. Considering a differential element within the fan (Fig. 35) then the previous rules for 1-D flow with weak waves shown in the previous sections canbe applied. The Mach Number changes from $M$ to $M + dM$ as the flow turns through an angle $dθ$. 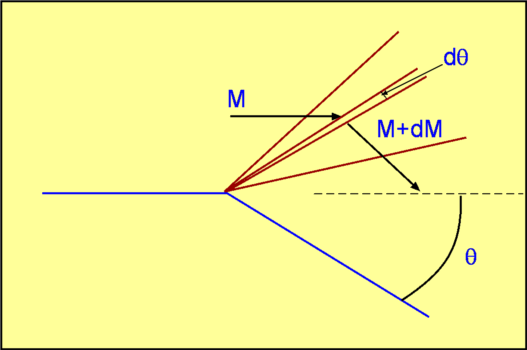 Figure 35 : Prandtl-Meyer Expansion, continued For a weak disturbance (Mach Wave), $$-dθ=√{M^2-1}{dw}/w$$ where $w$ is the initial flow velocity before the wave. On integrating it gives, $$-θ+\text"constant"= ∫√{M^2-1}{dw}/w = ν(M)$$ where a new function $ν$ has been introduced. This is called the Prandtl-Meyer function. Starting from the results of the previous 1-D flow section, $${dw}/w={dM}/M+{da}/a= {dM}/M(1/{1+{γ-1}/2M^2})$$ then, after manipulation and substitution, $$ν(M)=√{{γ+1}/{γ-1}}\tan^{-1}(√{{γ-1}/{γ+1}(M^2-1)})-\tan^{-1}(√{M^2-1})$$ The Prandtl-Meyer function is a significant tool for calculating supersonic flows. Note that for $M=1, ν=0$. For every Mach Number greater than one there is a unique Prandtl-Meyer function value. Tables for supersonic flow at the end of this section list $ν$ as a function of Mach Number. The practice, $ν$ is the angle through which a sonic flow should be turned in order to reach a Mach Number of $M$. In addition, a flow turning through an angle $θ$ will experience a change in Prandtl-Meyer function value of, $$ν_2=ν_1 + θ$$ With the knowledge of $ν, M_2$ can be calculated for any value of $θ$. This function can also calculate the Mach Number following an isentropic compression, $$ν_2=ν_1 - θ$$ 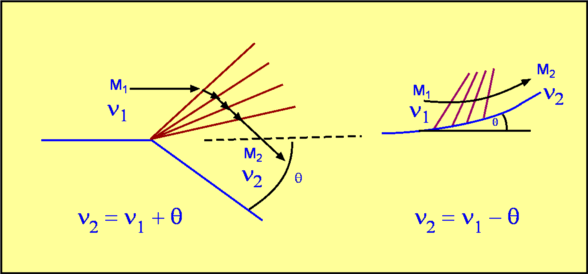 Figure 36 : Using Prandtl-Meyer Function It should be noted that $ν$ decreases in compression and increases in expansion. See Fig. 36 |